Union and Intersection of rounded objects

Using the same code as in Profiles and changing the definition of Object1 to two overlapping spheres

Fig1: field for two overlapping spheres.

 #declare R_Object1 =
   function(p,r,x,y,z){
      R_function(p,(sqrt(pow(x+1,2)+pow(y,2)+pow(z,2))-2)/r)
     +R_function(p,(sqrt(pow(x-1,2)+pow(y,2)+pow(z,2))-2)/r)
                      }

The top terrace shows where the fields of both spheres add together and the lower terrace the region where there is either sphere.

Intersect

Fig 2: Limiting the field to just the top terrace gives an Intersection.

 #declare R_Object1 =
   function(p,r,x,y,z){
     R_Intersection(
        R_function(p,(sqrt(pow(x+1,2)+pow(y,2)+pow(z,2))-2)/r)
       +R_function(p,(sqrt(pow(x-1,2)+pow(y,2)+pow(z,2))-2)/r)
                   )  }

Union

Fig 3: Limiting the field to the next terrace down gives a Union

 #declare R_Object1 =
   function(p,r,x,y,z){
     R_Union(
        R_function(p,(sqrt(pow(x+1,2)+pow(y,2)+pow(z,2))-2)/r)
       +R_function(p,(sqrt(pow(x-1,2)+pow(y,2)+pow(z,2))-2)/r)
            )         } 

Fig 4: Changing the sign of the radius has the effect of reversing the direction of the field:

 #declare R_Object1 = function(p,r,x,y,z){
   R_Intersection(
// Change the sign of r to change the direction of the field-V
      R_function(p,(sqrt(pow(x+1,2)+pow(y,2)+pow(z,2))-2)/   -r)
     +R_function(p,(sqrt(pow(x-1,2)+pow(y,2)+pow(z,2))-2)/   +r) ) }

Union of Rounded objects

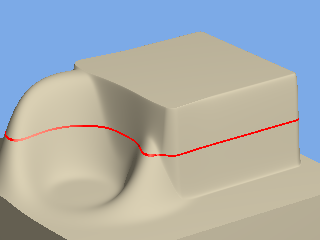Fig 5:  Objects with fields limited to one terrace using R_Union and R_Intersection can  be added:

#declare R_Object1 =
  function(p,r,x,y,z){
    +R_Union(
      +R_Intersection( R_Sphere(p,+r,1.8,x+1.2,y,z-.1)
                      +R_Sphere(p,-r,1.1,x+1.6,y,z+.2)
                     )
      +R_Cube(p,.2,1.7,x-1.2,y,z)
             )        }
#declare Profile = 0.6; // change this to change the shape of the corner. 0.6 gives very close to circular
#declare Radius = 1; // radius when the corner is circular and surfaces at right angles

This example uses the predefined R_Cube and R_Sphere included in  Rounded_Objects.inc listed on the Basics page

Intersection of rounded objects

Fig 6:  The intersection of two objects can also be obtained:

#declare R_Object1 =
  function(p,r,x,y,z){
    +R_Intersection(
      +R_Intersection( R_Sphere(p,+r,2.1,x+1.2,y,z-.1)
                      +R_Sphere(p,-r,1.3,x+1.6,y,z+.2)
                     )
      +R_Cube(p,.2,1.7,x-1.2,y,z)
                   ) }

Note that the diameters of the spheres have been increased in this example to make it more "interesting". One can see how the different corner profiles of the component R_Objects appear on the surface of the lump.